How to Understand & Calculate Statistical Significance [+ Example]
Recently, I was preparing to send an important bottom-of-funnel (BOFU) email to our audience. I had two subject lines and couldn‘t decide which one would perform better.
![How to Understand & Calculate Statistical Significance [+ Example]](https://www.hubspot.com/hubfs/how-to-calculate-statistical-significance-1-20250106-7754856.webp)
Recently, I was preparing to send an important bottom-of-funnel (BOFU) email to our audience. I had two subject lines and couldn‘t decide which one would perform better. Naturally, I thought, "Let’s A/B test them!" However, our email marketer quickly pointed out a limitation I hadn't considered: At first, this seemed counterintuitive. Surely 5,000 subscribers was enough to run a simple test between two subject lines? This conversation led me down a fascinating rabbit hole into the world of statistical significance and why it matters so much in marketing decisions. While tools like HubSpot’s free statistical significance calculator can make the math easier, understanding what they calculate and how it impacts your strategy is invaluable. Below, I’ll break down statistical significance with a real-world example, giving you the tools to make smarter, data-driven decisions in your marketing campaigns. Table of Contents In marketing, statistical significance is when the results of your research show that the relationships between the variables you're testing (like conversion rate and landing page type) aren't random; they influence each other. Statistical significance is like a truth detector for your data. It helps you determine if the difference between any two options — like your subject lines — is likely a real or random chance. Think of it like flipping a coin. If you flip it five times and get heads four times, does that mean your coin is biased? Probably not. But if you flip it 1,000 times and get heads 800 times, now you might be onto something. That's the role statistical significance plays: it separates coincidence from meaningful patterns. This was exactly what our email expert was trying to explain when I suggested we A/B test our subject lines. Just like the coin flip example, she pointed out that what looks like a meaningful difference — say, a 2% gap in open rates — might not tell the whole story. We needed to understand statistical significance before making decisions that could affect our entire email strategy. She then walked me through her testing process: “Seems straightforward, right?” she asked. Then she revealed where it gets tricky. She showed me a scenario: Imagine Group A had an open rate of 25% and Group B had an open rate of 27%. At first glance, it looks like Subject Line B performed better. But can we trust this result? What if the difference was just due to random chance and not because Subject Line B was truly better? This question led me down a fascinating path to understand why statistical significance matters so much in marketing decisions. Here's what I discovered: Through my research, I discovered that statistical significance helps you avoid acting on what could be a coincidence. It asks a crucial question: ‘If we repeated this test 100 times, how likely is it that we’d see this same difference in results?' If the answer is ‘very likely,’ then you can trust the outcome. If not, it's time to rethink your approach. Though I was eager to learn the statistical calculations, I first needed to understand a more fundamental question: when should we even run these tests in the first place? When deciding whether to run a test, use this decision framework to assess whether it’s worth the time and effort. Here’s how I break it down. Run tests when: Don’t run the test when: When you’re juggling multiple test ideas, I recommend using a prioritization matrix to focus on high-impact opportunities. High-priority tests: Low-priority tests: This framework ensures you focus your efforts where they matter most. But this led to my next big question: once you've decided to run a test, how do you actually determine statistical significance? Thankfully, while the math might sound intimidating, there are simple tools and methods for getting accurate answers. Let's break it down step by step. The first step is to identify what you’d like to test. This could be: The possibilities are endless, but simplicity is key. Start with a specific piece of content you want to improve, and set a clear goal — for example, boosting conversion rates or increasing views. While you can explore more complex approaches, like testing multiple variations (multivariate tests), I recommend starting with a straightforward A/B test. For this example, I’ll compare two variations of a landing page with the goal of increasing conversion rates. Pro tip: If you’re curious about the difference between A/B and multivariate tests, check out this guide on A/B vs. Multivariate Testing. When it comes to A/B testing, our resident email expert always emphasizes starting with a clear hypothesis. She explained that having a hypothesis helps focus the test and ensures meaningful results. In this case, since we’re testing two email subject lines, the hypothesis might look like this: Another key step is deciding on a confidence level before the test begins. A 95% confidence level is standard in most tests, as it ensures the results are statistically reliable and not just due to random chance. This structured approach makes it easier to interpret your results and take meaningful action. Once you’ve determined what you’d like to test, it’s time to start collecting your data. Since the goal of this test is to figure out which subject line performs better for future campaigns, you’ll need to select an appropriate sample size. For emails, this might mean splitting your list into random sample groups and sending each group a different subject line variation. For instance, if you’re testing two subject lines, divide your list evenly and randomly to ensure both groups are comparable. Determining the right sample size can be tricky, as it varies with each test. A good rule of thumb is to aim for an expected value greater than 5 for each variation. This helps ensure your results are statistically valid. (I’ll cover how to calculate expected values further down.) In researching how to analyze our email testing results, I discovered that while there are several statistical tests available, the Chi-Squared test is particularly well-suited for A/B testing scenarios like ours. This made perfect sense for our email testing scenario. A Chi-Squared test is used for discrete data, which simply means the results fall into distinct categories. In our case, an email recipient will either open the email or not open it — there's no middle ground. One key concept I needed to understand was the confidence level (also referred to as the alpha of the test). A 95% confidence level is standard, meaning there's only a 5% chance (alpha = 0.05) that the observed relationship is due to random chance. For example: “The results are statistically significant with 95% confidence” indicates that the alpha was 0.05, meaning there's a 1 in 20 chance of error in the results. My research showed that organizing the data into a simple chart for clarity is the best way to start. Since I’m testing two variations (Subject Line A and Subject Line B) and two outcomes (opened, did not open), I can use a 2x2 chart: Outcome Subject Line A Subject Line B Total Opened X (e.g., 125) Y (e.g., 135) X + Y Did Not Open Z (e.g., 375) W (e.g., 365) Z + W Total X + Z Y + W N This makes it easy to visualize the data and calculate your Chi-Squared results. Totals for each column and row provide a clear overview of the outcomes in aggregate, setting you up for the next step: running the actual test. While tools like HubSpot's A/B Testing Kit can calculate statistical significance automatically, understanding the underlying process helps you make better testing decisions. Let's look at how these calculations actually work: Once I’ve organized my data into a chart, the next step is to calculate statistical significance using the Chi-Squared formula. Here’s what the formula looks like: In this formula: To use the formula: This calculation tells you whether the differences between your groups are statistically significant or likely due to chance. Now, it’s time to calculate the expected values (E) for each outcome in your test. If there’s no relationship between the subject line and whether an email is opened, we’d expect the open rates to be proportionate across both variations (A and B). Let’s assume: Here’s how you organize the data in a table: Outcome Subject Line A Subject Line B Total Opened 500 (O) 500 (O) 1,000 Did Not Open 2,000 (O) 2,000 (O) 4,000 Total 2,500 2,500 5,000 Expected Values (E): To calculate the expected value for each cell, use this formula: E=(Row Total×Column Total)Grand TotalE = \frac{(\text{Row Total} \times \text{Column Total})}{\text{Grand Total}}E=Grand Total(Row Total×Column Total) For example, to calculate the expected number of opens for Subject Line A: E=(1,000×2,500)5,000=500E = \frac{(1,000 \times 2,500)}{5,000} = 500E=5,000(1,000×2,500)=500 Repeat this calculation for each cell: Outcome Subject Line A (E) Subject Line B (E) Total Opened 500 500 1,000 Did Not Open 2,000 2,000 4,000 Total 2,500 2,500 5,000 These expected values now provide the baseline you’ll use in the Chi-Squared formula to compare against the observed values. To calculate the Chi-Square value, compare the observed frequencies (O) to the expected frequencies (E) in each cell of your table. The formula for each cell is: χ2=(O−E)2E\chi^2 = \frac{(O - E)^2}{E}χ2=E(O−E)2 Steps: Let’s work through the data from the earlier example: Outcome Subject Line A (O) Subject Line B (O) Subject Line A (E) Subject Line B (E) (O−E)2/E(O - E)^2 / E(O−E)2/E Opened 550 450 500 500 (550−500)2/500=5(550-500)^2 / 500 = 5(550−500)2/500=5 Did Not Open 1,950 2,050 2,000 2,000 (1950−2000)2/2000=1.25(1950-2000)^2 / 2000 = 1.25(1950−2000)2/2000=1.25 Now sum up the (O−E)2/E(O - E)^2 / E(O−E)2/E values: χ2=5+1.25=6.25\chi^2 = 5 + 1.25 = 6.25χ2=5+1.25=6.25 This is your total Chi-Square value, which indicates how much the observed results differ from what was expected. What does this value mean? You’ll now compare this Chi-Square value to a critical value from a Chi-Square distribution table based on your degrees of freedom (number of categories - 1) and confidence level. If your value exceeds the critical value, the difference is statistically significant. Finally, I sum the results from all cells in the table to get my Chi-Square value. This value represents the total difference between the observed and expected results. Using the earlier example: Outcome (O−E)2/E(O - E)^2 / E(O−E)2/E for Subject Line A (O−E)2/E(O - E)^2 / E(O−E)2/E for Subject Line B Opened 5 5 Did Not Open 1.25 1.25 χ2=5+5+1.25+1.25=12.5\chi^2 = 5 + 5 + 1.25 + 1.25 = 12.5χ2=5+5+1.25+1.25=12.5 Compare your Chi-Square value to the distribution table. To determine if the results are statistically significant, I compare the Chi-Square value (12.5) to a critical value from a Chi-Square distribution table, based on: In this case: Since 12.5>3.8412.5 > 3.8412.5>3.84, the results are statistically significant. This indicates that there is a relationship between the subject line and the open rate. If the Chi-Square value were lower… For example, if the Chi-Square value had been 0.95 (as in the original scenario), it would be less than 3.84, meaning the results would not be statistically significant. This would indicate no meaningful relationship between the subject line and the open rate. As I dug deeper into statistical testing, I learned that interpreting results properly is just as crucial as running the tests themselves. Through my research, I discovered a systematic approach to evaluating test outcomes. Results are considered strong and actionable when they meet these key criteria: When results meet these criteria, the best practice is to act quickly: implement the winning variation, document what worked, and plan follow-up tests for further optimization. On the flip side, results are typically considered weak or inconclusive when they show these characteristics: In these cases, the recommended approach is to gather more data through retesting with a larger sample size or extending the test duration. My research revealed a practical decision framework for determining next steps after interpreting results. If the results are significant: If the results are not significant: This systematic approach ensures that every test, whether significant or not, contributes valuable insights to the optimization process. Through my research, I discovered that determining statistical significance comes down to understanding how to interpret the Chi-Square value. Here's what I learned. Two key factors determine statistical significance: Comparing values: The process turned out to be quite straightforward: you compare your calculated Chi-Square value to the critical value from a Chi-Square distribution table. For example, with df=1 and a 95% confidence level, the critical value is 3.84. What the numbers tell you: What happens if the results aren't significant? Through my investigation, I learned that non-significant results aren‘t necessarily failures — they’re common and provide valuable insights. Here's what I discovered about handling such situations. Review the test setup: Making decisions with non-significant results: When results aren't significant, there are several productive paths forward. After running your experiment, it’s essential to communicate the results to your team so everyone understands the findings and agrees on the next steps. Using the email subject line example, here’s how I’d approach reporting. When you’re reporting your findings, here are some best practices. By presenting results in a clear and actionable way, you help your team make data-driven decisions with confidence. What started as a simple desire to test two email subject lines led me down a fascinating path into the world of statistical significance. While my initial instinct was to just split our audience and compare results, I discovered that making truly data-driven decisions requires a more nuanced approach. Three key insights transformed how I think about A/B testing: First, sample size matters more than I initially thought. What seems like a large enough audience (even 5,000 subscribers!) might not actually give you reliable results, especially when you're looking for small but meaningful differences in performance. Second, statistical significance isn‘t just a mathematical hurdle — it’s a practical tool that helps prevent costly mistakes. Without it, we risk scaling strategies based on coincidence rather than genuine improvement. Finally, I learned that “failed” tests aren‘t really failures at all. Even when results aren’t statistically significant, they provide valuable insights that help shape future experiments and keep us from wasting resources on minimal changes that won't move the needle. This journey has given me a new appreciation for the role of statistical rigor in marketing decisions. While the math might seem intimidating at first, understanding these concepts makes the difference between guessing and knowing — between hoping our marketing works and being confident it does. Editor's note: This post was originally published in April 2013 and has been updated for comprehensiveness.

What is statistical significance?
Why is statistical significance important?

Here's Why Statistical Significance Matters
Sample size influences reliability: My initial assumption about our 5,000 subscribers being enough was wrong. When split evenly between the two groups, each subject line would only be tested on 2,500 people. With an average open rate of 20%, we‘d only see around 500 opens per group. I learned that’s not a huge number when trying to detect small differences like a 2% gap. The smaller the sample, the higher the chance that random variability skews your results.
The difference might not be real: This was eye-opening for me. Even if Subject Line B had 10 more opens than Subject Line A, that doesn‘t mean it’s definitively better. A statistical significance test would help determine if this difference is meaningful or if it could have happened by chance.
Making the wrong decision is costly: This really hits home. If we falsely concluded that Subject Line B was better and used it in future campaigns, we might miss opportunities to engage our audience more effectively. Worse, we could waste time and resources scaling a strategy that doesn't actually work.

How to Test for Statistical Significance: My Quick Decision Framework
Test Prioritization Matrix

How to Calculate and Determine Statistical Significance
1. Decide what you want to test.
2. Determine your hypothesis.

3. Start collecting your data.
4. Calculate Chi-Squared results.
Running the Chi-Squared test
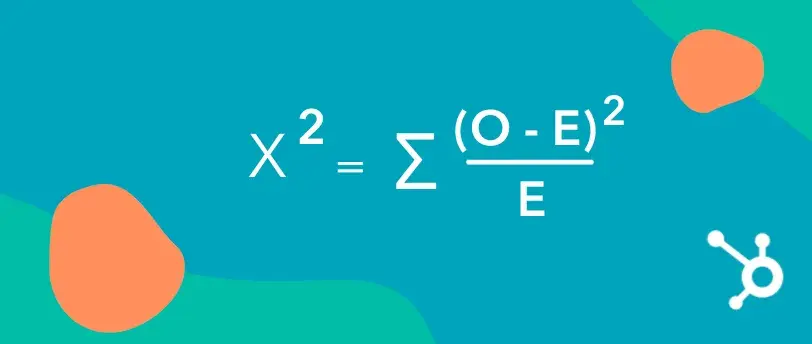
5. Calculate your expected values.
6. See how your results differ from what you expected.
7. Find your sum.
8. Interpret your results.
Strong Results (act immediately)
Weak Results (need more data)
Next Steps Decision Tree
9. Determine statistical significance.
10. Report on statistical significance to your team.
From Simple Test to Statistical Journey: What I Learned About Data-Driven Marketing

 Hollif
Hollif ![Instagram Engagement Report [Free Download]](https://no-cache.hubspot.com/cta/default/53/9294dd33-9827-4b39-8fc2-b7fbece7fdb9.png)








![How Nonprofits Can Use TikTok for Growth [Case Study + Examples]](https://blog.hubspot.com/hubfs/tiktok%20for%20nonprofits-1.jpg#keepProtocol)
![Best Times to Post on YouTube in 2022 [Research]](https://blog.hubspot.com/hubfs/best%20times%20to%20post%20on%20youtube.jpg#keepProtocol)

_1.png)








.jpg&h=630&w=1200&q=100&v=6e07dc5773&c=1)